Your Time has Finished

Close

    Close

    Your Score: %

    Average Score of All Users:

    You performed better than of students

    Section Breakdown

    Your Score Average of all Users Percentile
    BMAT 2012 S1

    BMAT 2012 S1

    Your score:

    Average score:

    You performed better than of students

    This section is Section 1 of 3.

    Speed as well as accuracy is important in this section. Work quickly, or you might not finish the paper. There are no penalties for incorrect responses, only marks for correct answers, so you should attempt all 35 questions. Each question is worth one mark.

    You must complete the answers within the time limit. Calculators are NOT permitted.

    Good Luck!

    Note – if press “End Exam” you can access full worked solutions for all past paper questions

    Six islands make up the Republic of Bondia.

    Island

    		 Area (km2) Population
    Brosnan 5079

    716,184

    Connery

    		 5816 931,896
    Craig 2474

    1,786,140

    Dalton

    		 5448 793,845
    Lazenby 1735

    1,458,253

    Moore

    		 5763 2,942,391
    Total 26315

    8,628,709
    1. Which island contains less than 10% of the population of Bondia, despite accounting for more than 20% of its area?
    • 0
    0

    Explanation

    The correct answer is D.

    20% of the total area of Bosnia is approximately 26000×0.2=5200km^2. So we can eliminate A,C and E because they each have an area less than 5200. 10% of the total population of Bondia is approximately 8600000×0.1=860000. Now we can eliminate B and F, because they each have a population less than 860000. Therefore the answer must be D.

    Post Comment

    People with pale skin may be lacking in vitamin D, which is important for healthy bones and Most people get enough vitamin D with short exposures to the sun (10 to 15 minutes a day). A small amount also comes from the diet, in foods like oily fish and dairy products. But people with pale skin do not seem to be able to get enough. Part of the reason might be that people who burn easily are more likely to cover up and avoid the sun. But some pale-skinned individuals are less able to make and process vitamin D in the body, regardless of how long they sit in the sun.

    Based on these findings, pale-skinned people should be added to the list of those for whom vitamin D supplements are recommended by the government. Certain groups are already identified as at higher risk of deficiency and needing supplements. This includes people with very dark skin, such as people of African-Caribbean and South Asian origin, and people who wear full-body coverings, as well as pregnant and breastfeeding women, the elderly and people who avoid the sun.

    2. Which of the following best expresses the main conclusion of the passage?
    • 0
    0

    Explanation

    The correct answer is C.

    The first paragraph in the passage focuses on providing evidence to support the final conclusion that ‘pale-skinned people should be added to the list of those for whom vitamin D supplements are recommended by the government’. This is paraphrased in statement C.

    Statement A is incorrect because the main conclusion of the passage does not state that pale-skinned people need more sunlight exposure. Conversely, it highlights that even ‘regardless of how long they sit in the sun’ they are less able to make and process vitamin D in the body. Therefore this recommendation is in itself incorrect, based on the evidence.

    Statement D is incorrect because there is no mention of the increased risk of skin cancer from increased sun exposure.

    Statement E is incorrect because it cannot be inferred that dark skinned people need more Vitamin D than pale-skinned people despite both being identified as high risk groups for vitamin D deficiency.

    Post Comment

    I wish to tile part of my wall with a mixture of five patterned, cross-shaped tiles. I want to use the same number of each tile, but end up with the same area of each pattern.

    3. Which of the following six tiles can I not include?
    • 1
    2

    Explanation

    The correct answer is F.

    Let’s pick 5 of the 6 tiles and see if we have the same number of squares of each pattern. Choosing all the tiles except F, we will find that we have 5 squares of each pattern (stripe, spots, check, black and white). None of the other combinations of tiles will give the same number of squares of each pattern.

    Post Comment
    Laiba Medicmind Tutor

    Sat, 10 Sep 2022 12:30:24

    Answer F has four pattern so the answer option is wrong

    Electric engines are more efficient than petrol engines in converting fuel into mechanical power, thus they are more economical in fuel use. But their electricity has to come from somewhere. The UK electricity grid is powered by a mix of sources: coal, gas and nuclear with a few renewables thrown in. If you make extra demand in order to fuel electric cars, only fossil fuels, which produce emissions of CO2, can provide the extra capacity. Wind turbines cannot turn any faster than wind speed allows, and extra capacity from nuclear power will be possible only when new nuclear power plants are built.

    4. Which one of the following can be drawn as a conclusion from the above passage?
    • 0
    0

    Explanation

    The correct answer is B.

    The paragraph explains that to be able to power the increase in the UK’s electricity grid in order to fuel electric cars, there needs to be an increase in fossil fuel consumption which simultaneously produces increased carbon dioxide emissions. Therefore, in order to meet this increased demand in electricity, there will be an increase in carbon dioxide emissions being produced. This is summarised in statement B.

    Statement A is incorrect because the electricity needed to power electric cars can be provided by the UK’s electricity grid, given that it’s powered energy sources increase.

    Statement C is incorrect as the main conclusion does not refer to the potential future limitations of wind power. Additionally, the word ‘never’ in the statement is too bold to be correct.

    Statement D is also incorrect because it cannot be inferred that because electric engines are more economical than petrol engines that they are also will increase carbon dioxide emissions.

    Post Comment

    My brother and I have commissioned a landscape gardener to redesign the back garden of the house into which our parents have recently The diagram below shows the new layout:

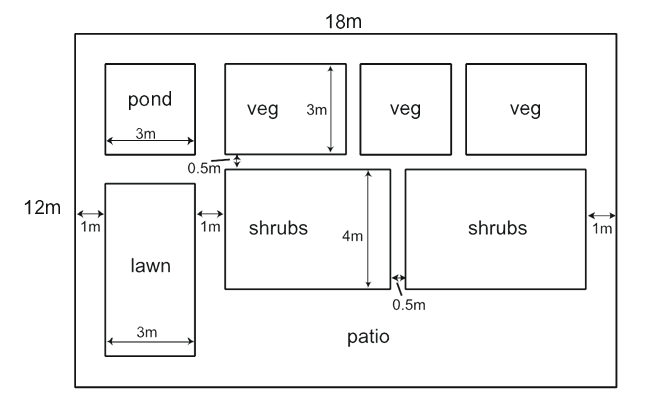
    The paths are 1m wide, apart from those which run between the veg areas and the shrub areas, which are 0.5m in width.

    5. How many 0.5m square paving slabs will be needed to make the patio and all the paths?
    • 0
    0

    Explanation

    The correct answer is E.

    The total area of the garden is 12×18=216m^2. Now we need to subtract the areas of the pond, lawn, veg and shrub areas to calculate the area of the patio and paths. The combined length of the veg areas is 18-(3+1+1+1+0.5+0.5)=11m; the combined length of the shrub areas is 18-(3+1+1+1+0.5)=11.5m, and the height of the lawn is 12-(3+1+1+1)=6m The areas are as follows: pond=3×3=9, veg areas=11×3=33, lawn=3×6=18 and shrub areas=11.5×4=46. Therefore the total area of the patio and paths is 216-(9+33+18+46)=216-106=110m^2. The area of each paving slab is 0.5×0.5=0.25m^2, therefore 110/0.25=440 slabs would be needed to cover the patio and paths.

    Post Comment

    The Organisation for Economic Co-operation and Development (OECD) has released data from a study of 15 year olds in the principal industrialised countries. It shows unequivocally that teenage students whose parents discuss political or social issues with them, either weekly or daily, score 28 points higher at reading (on average) than those whose parents discuss these issues less often or not at all. Other factors were also associated with better reading ability: discussing books or television programmes, eating main meals together at a table and spending time talking to children. Discussing news and serious issues showed the strongest association, so if parents spend time discussing these issues with their children they will help their children read well.

    6. Which of the following best expresses the flaw in the argument above?
    • 0
    0

    Explanation

    The correct answer is E.

    C1: if parents spend time discussing these issues with their children they will help their children read well.

    This is a correlation not causation type flaw. The argument suggests a direct link between discussion and reading ability. A, B, C are irrelevant and in the case of A and C, the facts in the statements are not mentioned in the text. D is not a feasible flaw based on the argument.

    Post Comment

    The pattern below is to be used to tile a very large floor. It consists of hexagonal, square and triangular shaped tiles.

    7. If tiling a sufficiently large area, what ratio of the three shapes of tile is needed?
    • 0
    1

    Explanation

    The correct answer is A.

    Counting the number of each shape in the diagram, there are 19 squares, 16 triangles and 4 hexagons, But the diagram shows more than a repeating unit (the combination of shapes that would continue to produce the pattern when repeated over and over). I have highlighted the repeating unit below:

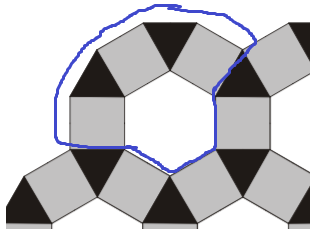
    This consists of 1 hexagon, 2 triangles and 3 squares.

    Post Comment

    The following table shows the infection statistics of Clostridium difficile infection (CdI) for a number of organisations for 2009 and 2010.

    		 2009 2010
    Organ- isation Types

    of hospital

    		 Number

    of hospitals

    		 Patient days Cases Rate of infection* Number of hospitals Patient days Cases

    Rate of infection*

    1

    		 L,S 3 56,867 0 0 3 53,967 1 1.85
    2 S 1 16,330 1 6.12 1 16,163 0

    0

    3

    		 L,S 56 540,891 26 4.81 59 543,042 25 4.60
    4 L 1 11,549 0 0 1 30,432 3

    9.86

    5

    		 DC,TC 9 70,009 4 5.71 9 69,397 2 2.88
    6 L 4 178,556 3 1.68 7 180,805 6

    3.32

    7

    		 L 1 18,155 0 0 1 18,931 1 5.28
    8 L,S 29 320,009 2 0.62 29 317,876 5

    1.57

    9

    		 L,S,TC 32 110,925 3 2.70 31 136,586 2 1.46
    10 L 1 82,293 1 1.22 1 80,456 3

    3.73

    11

    		 L,S 33 409,574 12 2.93 33 394,693 12 3.04
    12 L 1 18,278 5 27.36 1 16,792 6

    35.73

    13

    		 L 1 29,202 12 41.09 1 30,308 11

    36.29

    * rate of infection is calculated as number of cases per 100,000 patient days.

    The codes for the different types of hospital are L (large), S (small), DC (diagnosis centre) and TC (treatment centre). The number of patient days is calculated from the number of days that patients were in hospital. For example, a day case (a patient who was not in hospital overnight) would count as 1 patient day and a patient staying in the hospital over 3 consecutive nights would count as 4 patient days. The rate given is the rate per 100,000 patient days.

    8. What is the overall rate (over both years) per 100,000 patient days for organisation 4 in the table?
    • 0
    0

    Explanation

    The correct answer is C.

    There were infections recorded for organisation 4 in 2009, so over the 2 years the number of cases was 3. The total number of patient days in organisaation 4 over the 2 years is 11549+30432, which can be approximated as 12000+30000=42000 patient days. So per 100000 patient days, there were 100000/42000×3=50/21×3=50/7=7.14, which is closest to 7.15 out of the answer options given.

    Post Comment
    s Medicmind Tutor

    Wed, 04 Oct 2023 13:03:00

    where did the 50 come from?

    The following table shows the infection statistics of Clostridium difficile infection (CdI) for a number of organisations for 2009 and 2010.

    		 2009 2010
    Organ- isation Types

    of hospital

    		 Number

    of hospitals

    		 Patient days Cases Rate of infection* Number of hospitals Patient days Cases

    Rate of infection*

    1

    		 L,S 3 56,867 0 0 3 53,967 1 1.85
    2 S 1 16,330 1 6.12 1 16,163 0

    0

    3

    		 L,S 56 540,891 26 4.81 59 543,042 25 4.60
    4 L 1 11,549 0 0 1 30,432 3

    9.86

    5

    		 DC,TC 9 70,009 4 5.71 9 69,397 2 2.88
    6 L 4 178,556 3 1.68 7 180,805 6

    3.32

    7

    		 L 1 18,155 0 0 1 18,931 1 5.28
    8 L,S 29 320,009 2 0.62 29 317,876 5

    1.57

    9

    		 L,S,TC 32 110,925 3 2.70 31 136,586 2 1.46
    10 L 1 82,293 1 1.22 1 80,456 3

    3.73

    11

    		 L,S 33 409,574 12 2.93 33 394,693 12 3.04
    12 L 1 18,278 5 27.36 1 16,792 6

    35.73

    13

    		 L 1 29,202 12 41.09 1 30,308 11

    36.29

    * rate of infection is calculated as number of cases per 100,000 patient days.

    The codes for the different types of hospital are L (large), S (small), DC (diagnosis centre) and TC (treatment centre). The number of patient days is calculated from the number of days that patients were in hospital. For example, a day case (a patient who was not in hospital overnight) would count as 1 patient day and a patient staying in the hospital over 3 consecutive nights would count as 4 patient days. The rate given is the rate per 100,000 patient days.

    9. What is the largest proportion of cases in 2009 that came from a single organisation?
    • 0
    0

    Explanation

    The correct answer is D.

    The total number of cases across all organisations in 2009 was: 1+26+4+3+2+3+1+12+5+12=69. The highest number of cases from a single organisation in this year was 26, so the largest proportion of cases that came from a single organisation in 2009 was 26/69=0.38 or 38%.

    Post Comment

    The following table shows the infection statistics of Clostridium difficile infection (CdI) for a number of organisations for 2009 and 2010.

    		 2009 2010
    Organ- isation Types

    of hospital

    		 Number

    of hospitals

    		 Patient days Cases Rate of infection* Number of hospitals Patient days Cases

    Rate of infection*

    1

    		 L,S 3 56,867 0 0 3 53,967 1 1.85
    2 S 1 16,330 1 6.12 1 16,163 0

    0

    3

    		 L,S 56 540,891 26 4.81 59 543,042 25 4.60
    4 L 1 11,549 0 0 1 30,432 3

    9.86

    5

    		 DC,TC 9 70,009 4 5.71 9 69,397 2 2.88
    6 L 4 178,556 3 1.68 7 180,805 6

    3.32

    7

    		 L 1 18,155 0 0 1 18,931 1 5.28
    8 L,S 29 320,009 2 0.62 29 317,876 5

    1.57

    9

    		 L,S,TC 32 110,925 3 2.70 31 136,586 2 1.46
    10 L 1 82,293 1 1.22 1 80,456 3

    3.73

    11

    		 L,S 33 409,574 12 2.93 33 394,693 12 3.04
    12 L 1 18,278 5 27.36 1 16,792 6

    35.73

    13

    		 L 1 29,202 12 41.09 1 30,308 11

    36.29

    * rate of infection is calculated as number of cases per 100,000 patient days.

    The codes for the different types of hospital are L (large), S (small), DC (diagnosis centre) and TC (treatment centre). The number of patient days is calculated from the number of days that patients were in hospital. For example, a day case (a patient who was not in hospital overnight) would count as 1 patient day and a patient staying in the hospital over 3 consecutive nights would count as 4 patient days. The rate given is the rate per 100,000 patient days.

    Not all organisations had reported all data for 2010 by the time that the table was completed (so 2010 figures only include data to the end of November).

    10. If the number of patient days per month is constant and organisation 2 did have one case in December 2010, what would the rate of infection for that organisation in that year have been?
    • 0
    0

    Explanation

    The correct answer is B.

    The number of patient days per month for organisation 2 in Jan-Nov 2010 would be 16163/11~16100/11=1464. So the total number of patient days from Jan-Dec 2010 would have been approximately 1464×12=17568. The rate of infection is calculated as the number of cases per 100000 patient days, and if there was only 1 case in December the rate of infection would be 1/17568×100000=5.69. As we initially rounded down the number of patient days, this is a slight overestimate, so the answer must be 5.67.

    Post Comment

    The following table shows the infection statistics of Clostridium difficile infection (CdI) for a number of organisations for 2009 and 2010.

    		 2009 2010
    Organ- isation Types

    of hospital

    		 Number

    of hospitals

    		 Patient days Cases Rate of infection* Number of hospitals Patient days Cases

    Rate of infection*

    1

    		 L,S 3 56,867 0 0 3 53,967 1 1.85
    2 S 1 16,330 1 6.12 1 16,163 0

    0

    3

    		 L,S 56 540,891 26 4.81 59 543,042 25 4.60
    4 L 1 11,549 0 0 1 30,432 3

    9.86

    5

    		 DC,TC 9 70,009 4 5.71 9 69,397 2 2.88
    6 L 4 178,556 3 1.68 7 180,805 6

    3.32

    7

    		 L 1 18,155 0 0 1 18,931 1 5.28
    8 L,S 29 320,009 2 0.62 29 317,876 5

    1.57

    9

    		 L,S,TC 32 110,925 3 2.70 31 136,586 2 1.46
    10 L 1 82,293 1 1.22 1 80,456 3

    3.73

    11

    		 L,S 33 409,574 12 2.93 33 394,693 12 3.04
    12 L 1 18,278 5 27.36 1 16,792 6

    35.73

    13

    		 L 1 29,202 12 41.09 1 30,308 11

    36.29

    * rate of infection is calculated as number of cases per 100,000 patient days.

    The codes for the different types of hospital are L (large), S (small), DC (diagnosis centre) and TC (treatment centre). The number of patient days is calculated from the number of days that patients were in hospital. For example, a day case (a patient who was not in hospital overnight) would count as 1 patient day and a patient staying in the hospital over 3 consecutive nights would count as 4 patient days. The rate given is the rate per 100,000 patient days.

    11. Which of the following statements can be reliably concluded from the data in the table?
    • 1
    0

    Explanation

    The correct answer is E.

    Statements A and B cannot be concluded from the data, and counting the number of cases in both large and small hospitals shows that C is incorrect as well. We cannot determine if Cdl occurs in DC and TC type hospitals because each organisation these two types of hospital are apart of on the table also has at least 1 other type of hospital as well, so we don’t know which type of hospital the Cdl cases in these multi-hospital-type organisations is occuring in. Therefore D cannot be concluded either, Hence, none of the 4 statements can be concluded.

    Post Comment

    A bus service runs between Pafaka Airport and the centre of Pafaka. The journey in either direction takes 50 minutes.

    The timetable for the service is compiled in conjunction with flight timetables, and at present is as follows:

    Departure times from Pafaka Airport
    Mon Tues Wed Thur Fri Sat

    Sun

    11:30

    		 09:30 09:15 09:15 06:15 08:00 08:45
    14:25 11:30 11:10 11:30 09:15 11:30

    11:30

    17:45

    		 14:20 14:00 14:20 11:30 14:30 14:30
    19:40 19:00 19:00 17:20 14:40 17:00

    17:30

    		18:30 15:25 19:00 19:30
    19:20 17:00

    		19:00

    Departure times from Pafaka Centre
    Mon Tues Wed Thur Fri Sat

    Sun

    14:30

    		 14:30 12:00 14:30 07:05 14:30 11:45
    15:25 15:25 14:30 15:20 11:40 15:30

    14:30

    16:35

    		 16:35 16:45 16:30 12:30 16:30 15:30
    22:15 20:00 22:15 19:45 14:30 22:20

    16:30

    		22:15 20:20 15:30 20:30
    21:25 16:30

    22:15

    		22:40 20:00
    22:15

    Nicola lives within walking distance of the Airport bus stop, and uses the service when she wants to go shopping in Pafaka. She intends to do this next Thursday. She will take the first bus of the day from the Airport, and stay in Pafaka for as long as possible, but she wants to be back at the Airport before 17:00.

    12. How long after arriving in the centre of Pafaka will Nicola have to catch the bus to the Airport?
    • 0
    0

    Explanation

    The correct answer is B.

    She will take the first bus of the day from the airport on Thursday, which departs at 09:15. She wants to get back at the airport before 17:00, and the journey time is 50 minutes, therefore she must take the latest bus on Thursday departing from Pafaka centre before 17:00-50min=16:10. The latest bus departing before 16:10 from the centre leaves at 15:20. Nicola will arrive in the centre after catching her 09:15 bus at 09:15+50min=10:05 and catches the bus from the centre at 15:20, so the time between these is 15:20-10:05=5hrs and 15min, answer B.

    Post Comment

    The unusual weather the UK has experienced over the past few years – very dry warm springs and very cold winters – is what one would expect if the melting of Arctic ice were influencing our weather. And indeed, over the same period the Arctic has undergone its most dramatic shrinkage of sea ice. This means that the Arctic Ocean is warming, which can upset the global balance between cold Arctic air and warm tropical air.

    13. Which one of the following can be drawn as a conclusion from the above passage?
    • 0
    0

    Explanation

    The correct answer is D.

    Statement D is correct because it is the only conclusion that is not too bold. The phrase ‘could have been caused’ is used in a similar way in the paragraph’s last sentence with the words ‘ which can upset…’. This makes the link between the weather changes in the UK and the shrinkage of sea ice possible but not 100% certain.

    Statements A-C are too bold with the use of words such as ‘only’, ‘if the artic ice…’ and ‘must have’ respectively. This make it out to be that the link between the two variables mentioned is certain, making the statements incorrect.

    Post Comment

    The net shown below was cut out and folded to make a cube.

    14. Which one of the following cubes was formed from this net?
    • 0
    2

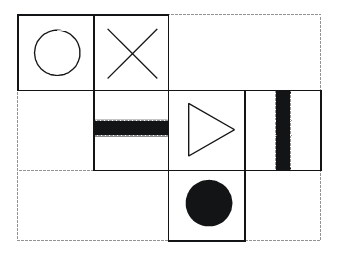
    Explanation

    The correct answer is D.

    The following explanations are assuming all of the other faces in A-E are in the correct positions according to the net. 

    A is incorrect because the black line on the top face in A would be positioned vertically rather than horizontally. B is incorrect because the black line on the right face in B would be positioned horizontally rather than vertically. C is incorrect because the black line on the top face in C would be positioned horizontally rather than vertically. E is incorrect because the black line on the right face in E would be positioned vertically instead of horizontally. 

    Therefore D is correct.

    Post Comment

    Oxytocin, known as the ‘love hormone’, is a hormone that is released in mothers’ bodies during Research has shown that when people are exposed to it by means of a nasal spray they can become better at recognising the emotions of others, and are more likely to perceive others as trustworthy and approachable. As a result of its apparently positive influence on sociability, there is optimism that it could help to treat conditions such as autism and schizophrenia. Oxytocin sprays are readily available online, and are being used by parents to treat children with autism. Although clinical trials are now under way, the use of oxytocin as a treatment has not yet been approved. So parents of children with autism are damaging their children’s health by using the sprays.

    15. Which one of the following, if true, would weaken the above argument?
    • 2
    0

    Explanation

    The correct answer is C.

    The main conclusion of the passage is that ‘parents of children with autism are damaging their children’s health by using the sprays,’ since oxytocin is not an approved treatment form for autism. Statement C, if considered true, is therefore correct. If there are negligible amounts of oxytocin in the sprays (considered to be ‘too low to have any effect in children’) then this weakens the argument as having low effects may lead to reduced levels of damage produced by oxytocin.

    Statement A, if considered true, acts to strengthen the final conclusion as the feeling of envy could be considered a negative attribute.

    Statement B is incorrect because this too would to some extent strengthen the argument as oxytocin sprays could be considered to damage the health of children if no prior tests have been conducted on them.

    Statement D is incorrect because there is no mention of the differing levels of oxytocin in different cultures.

    Statement E is also incorrect as this would strengthen the final conclusion.

    Post Comment

    This is the floor of my conservatory:

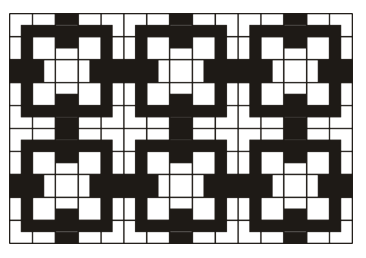
    It contains the following four individual tile patterns:

    16. What percentage of the floor of my conservatory is black?
    • 0
    0

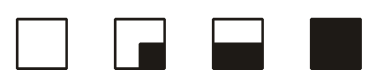
    Explanation

    The correct answer is C.

    There are 25 tiles in each repeating unit of the floor pattern. As we are asked for a proportion, we only need to consider the tiles in one of the repeating units, as the proportion of black will be the same as for the entire floor. In one repeating unit of 25 tiles, there are 5 plain white tiles, 4 quarter black tiles, 12 half black tiles, and 4 plain black tiles. If we considered the total area of black as a number of tiles, the number of black tiles would be (4×1/4)+(12×1/2)+4=1+6+4=11 black tiles per 25 tiles. Therefore the proportion of floor which is black must be 11/25=0.44 or 44%.

    Post Comment

    Patients admitted to hospital as an emergency at the weekend have a higher chance of dying than those who are brought in during the week, according to a study which showed that the death rate among emergency admissions increased by 7% at the weekend.

    Staffing levels are often lower at weekends, with fewer senior medical staff around, and some specialist services are less available. This may be contributing to the increase in mortality rates on Saturdays and Sundays. As well as lower staffing levels in hospitals, there may be a reduced service in specialist community and primary care services at the weekend, which may result in some terminally ill patients being admitted to hospital and dying there (instead of at home) at the weekends.

    1. Improved staffing levels in hospitals at weekends would reduce death

    2. Weekend provision of community and primary care services should be

    3. Fewer patients should be admitted to hospital at times when staffing levels are low.

    17. Which of the following could be drawn as a conclusion from the passage above?
    • 0
    0

    Explanation

    The correct answer is G.

    Statement 1 is incorrect as it cannot be assumed that improving staffing levels at the weekends would reduce death rates in hospitals. It is fair to assume that this statement is correct from the phrase ‘staffing levels are often lower at weekends..’ However, this is followed by the sentence ‘This may be contributing to the increase in mortality rates…’ The use of the word ‘may’ implies that it is a possibility but not 100% certain, which is what statement 1 implies.

    Statement 2 is incorrect because the passage explains that patients are admitted to hospital instead of dying at home due to lack of specialist community and primary care services. This means that the weekend mortality rates in hospitals are above what they should be and so increasing specialised community based care would not affect the true mortality rate in hospitals.

    Statement 3 is incorrect because it assumes that lower levels of staffing are the cause for increased deaths. But this cannot be assumed for certain as stated by the words ‘fewer patients should be admitted…’. The use of such words is too bold.

    Post Comment

    A survey of households in a town showed that (allowing for sampling errors) between 75% and 85% owned a dishwasher, between 35% and 40% owned a tumble dryer and less than 5% owned neither.

    18. How many people own both a tumble dryer and a dishwasher?
    • 0
    1

    Explanation

    The correct answer is A.

    To maximise the number of people who owned both a tumble dryer and a dishwasher we need to maximise the number of people who had each of these items, taking them as 40% and 85% respectively. We can also minimise the percentage who had neither item, taking it as 0%. Therefore the upper bound for the number of people having both items would be (40+85+5)-100=30%. 

    To minimise the number of people who owned both items we do the opposite, minimising the proportion who had both items and maximising those who had neither item. So the calculation would be (35+75)-100=10%.

    Post Comment
    Moniba Medicmind Tutor

    Sat, 15 Oct 2022 14:07:05

    Hi, I'm confused why 5 has been added to the upper bound when it was assumed to be 0% for for those who had neither item And then why 5 was not added for the lower bound when it was assumed to be 5%?

    NHS Information Centre Report on Ambulance services in England 2011: Executive summary

    The total number of emergency calls was 8.08 million, a 209,608 (2.7%) increase over 2010 when there were 7.87 million.

    Of these, 6.61 million calls (81.8%) resulted in an emergency response arriving at the scene of the incident, a 191,310 (3.0%) increase over 2010 when there were 6.42 million.

    Of the incidents attended the number classed as category A was 2.23 million equal to 7%, the figure in 2010 was 2.08 million (32.4%). The number of incidents attended as class B was 2.63 million (39.8%), this is compared with 2.61 million (40.7%) in 2010.

    The percentage of category A incidents that resulted in an emergency response arriving at the scene of the incident within 8 minutes in 2011 was 74.9% compared to 74.3% in 2010.

    The percentage of category A incidents that resulted in an ambulance vehicle capable of transporting the patient arriving at the scene within 19 minutes was 96.7% compared to 8% in 2010. For category B incidents this was 91.2%.(1)

    The number of emergency patient journeys was 4.87 million, over 172,000 (3.7%) more than in 2010 when there were 4.70 million.

    76 million patients were treated at the scene and did not need onward transportation. This is an increase of 164,224 (10.3%) since 2010.

    There were 239,446 category C calls resolved with telephone advice, equating to 8.7% of all category C calls, an increase of 18,436 (8.3%) since 2010.

    (1)Due to changes in the category B 19 minute definitions for 2011 this data is not fully comparable with previous years.

    Definitions

    Category A: Presenting conditions, which may be immediately life threatening and should receive an emergency response within 8 minutes irrespective of location in 75% of cases. Presenting conditions, which require a fully equipped ambulance vehicle to attend the incident, must have an ambulance vehicle arrive within 19 minutes of the request for transport being made in 95% of cases, unless the control room decides that an ambulance is not required.

    Category B: Presenting conditions, which though serious are not immediately life threatening and must receive a response within 19 minutes in 95% of cases.

    Category C: Presenting conditions which are not immediately serious or life threatening. For these calls the response time standards are not set nationally but are locally determined.

    19. How many category A calls were responded to but not within 8 minutes in 2011?
    • 0
    0

    Explanation

    The correct answer is B.

    The percentage of category A calls that were responded to within 8 minutes in 2011 was 74.9%. Therefore the percentage that were not responded to within 8 minutes was 100-74.9=25.1%. There were 2.23 million category A incidents in 2011, so the number of category A incidents that were responded to in over 8 minutes was 2.23×0.251=0.56. Or 56%.

    Post Comment

    NHS Information Centre Report on Ambulance services in England 2011: Executive summary

    The total number of emergency calls was 8.08 million, a 209,608 (2.7%) increase over 2010 when there were 7.87 million.

    Of these, 6.61 million calls (81.8%) resulted in an emergency response arriving at the scene of the incident, a 191,310 (3.0%) increase over 2010 when there were 6.42

    Of the incidents attended the number classed as category A was 2.23 million equal to 7%, the figure in 2010 was 2.08 million (32.4%). The number of incidents attended as class B was 2.63 million (39.8%), this is compared with 2.61 million (40.7%) in 2010.

    The percentage of category A incidents that resulted in an emergency response arriving at the scene of the incident within 8 minutes in 2011 was 74.9% compared to 74.3% in

    The percentage of category A incidents that resulted in an ambulance vehicle capable of transporting the patient arriving at the scene within 19 minutes was 96.7% compared to 8% in 2010. For category B incidents this was 91.2%.(1)

    The number of emergency patient journeys was 4.87 million, over 172,000 (3.7%) more than in 2010 when there were 4.70 million.

    76 million patients were treated at the scene and did not need onward transportation. This is an increase of 164,224 (10.3%) since 2010.

    There were 239,446 category C calls resolved with telephone advice, equating to 8.7% of all category C calls, an increase of 18,436 (8.3%) since 2010.

    (1)Due to changes in the category B 19 minute definitions for 2011 this data is not fully comparable with previous years.

    Definitions

    Category A: Presenting conditions, which may be immediately life threatening and should receive an emergency response within 8 minutes irrespective of location in 75% of cases. Presenting conditions, which require a fully equipped ambulance vehicle to attend the incident, must have an ambulance vehicle arrive within 19 minutes of the request for transport being made in 95% of cases, unless the control room decides that an ambulance is not required.

    Category B: Presenting conditions, which though serious are not immediately life threatening and must receive a response within 19 minutes in 95% of cases.

    Category C: Presenting conditions which are not immediately serious or life threatening. For these calls the response time standards are not set nationally but are locally determined.

    20. Which one of the following pie charts correctly represents the number of accidents attended in 2011 by category?
    • 1
    0

    Explanation

    The correct answer is D.

    Post Comment
    Shalise Zhini Medicmind Tutor

    Tue, 02 Nov 2021 21:36:19

    Hello, fuck you.

    NHS Information Centre Report on Ambulance services in England 2011: Executive summary

    The total number of emergency calls was 8.08 million, a 209,608 (2.7%) increase over 2010 when there were 7.87 million.

    Of these, 6.61 million calls (81.8%) resulted in an emergency response arriving at the scene of the incident, a 191,310 (3.0%) increase over 2010 when there were 6.42 million.

    Of the incidents attended the number classed as category A was 2.23 million equal to 7%, the figure in 2010 was 2.08 million (32.4%). The number of incidents attended as class B was 2.63 million (39.8%), this is compared with 2.61 million (40.7%) in 2010.

    The percentage of category A incidents that resulted in an emergency response arriving at the scene of the incident within 8 minutes in 2011 was 74.9% compared to 74.3% in 2010.

    The percentage of category A incidents that resulted in an ambulance vehicle capable of transporting the patient arriving at the scene within 19 minutes was 96.7% compared to 8% in 2010. For category B incidents this was 91.2%.(1)

    The number of emergency patient journeys was 4.87 million, over 172,000 (3.7%) more than in 2010 when there were 4.70 million.

    76 million patients were treated at the scene and did not need onward transportation. This is an increase of 164,224 (10.3%) since 2010.

    There were 239,446 category C calls resolved with telephone advice, equating to 8.7% of all category C calls, an increase of 18,436 (8.3%) since 2010.

    (1)Due to changes in the category B 19 minute definitions for 2011 this data is not fully comparable with previous years.

    Definitions

    Category A: Presenting conditions, which may be immediately life threatening and should receive an emergency response within 8 minutes irrespective of location in 75% of cases. Presenting conditions, which require a fully equipped ambulance vehicle to attend the incident, must have an ambulance vehicle arrive within 19 minutes of the request for transport being made in 95% of cases, unless the control room decides that an ambulance is not required.

    Category B: Presenting conditions, which though serious are not immediately life threatening and must receive a response within 19 minutes in 95% of cases.

    Category C: Presenting conditions which are not immediately serious or life threatening. For these calls the response time standards are not set nationally but are locally determined.

    The total number of calls in 2011 was 8.08 million, but there were only 6.61 million transported or treated at the scene.

    21. Which of the following is the correct explanation for this difference?
    • 0
    0

    Explanation

    The correct answer is B.

    The statement refers to the calls that were responded to at all, not in a given time frame, so A is incorrect. 

    Some non-genuine emergencies may still have been responded to as if they were not emergencies, so C is incorrect. 

    In 2011 there were 239446/0.087=2752253=2.75 million category C calls, not 1.47 millions, therefore D is incorrect.

    Hence B is the correct explanation.

    Post Comment

    NHS Information Centre Report on Ambulance services in England 2011: Executive summary

    The total number of emergency calls was 8.08 million, a 209,608 (2.7%) increase over 2010 when there were 7.87 million.

    Of these, 6.61 million calls (81.8%) resulted in an emergency response arriving at the scene of the incident, a 191,310 (3.0%) increase over 2010 when there were 6.42 million.

    Of the incidents attended the number classed as category A was 2.23 million equal to 7%, the figure in 2010 was 2.08 million (32.4%). The number of incidents attended as class B was 2.63 million (39.8%), this is compared with 2.61 million (40.7%) in 2010.

    The percentage of category A incidents that resulted in an emergency response arriving at the scene of the incident within 8 minutes in 2011 was 74.9% compared to 74.3% in 2010.

    The percentage of category A incidents that resulted in an ambulance vehicle capable of transporting the patient arriving at the scene within 19 minutes was 96.7% compared to 8% in 2010. For category B incidents this was 91.2%.(1)

    The number of emergency patient journeys was 4.87 million, over 172,000 (3.7%) more than in 2010 when there were 4.70 million.

    76 million patients were treated at the scene and did not need onward transportation. This is an increase of 164,224 (10.3%) since 2010.

    There were 239,446 category C calls resolved with telephone advice, equating to 8.7% of all category C calls, an increase of 18,436 (8.3%) since 2010.

    (1)Due to changes in the category B 19 minute definitions for 2011 this data is not fully comparable with previous years.

    Definitions

    Category A: Presenting conditions, which may be immediately life threatening and should receive an emergency response within 8 minutes irrespective of location in 75% of cases. Presenting conditions, which require a fully equipped ambulance vehicle to attend the incident, must have an ambulance vehicle arrive within 19 minutes of the request for transport being made in 95% of cases, unless the control room decides that an ambulance is not required.

    Category B: Presenting conditions, which though serious are not immediately life threatening and must receive a response within 19 minutes in 95% of cases.

    Category C: Presenting conditions which are not immediately serious or life threatening. For these calls the response time standards are not set nationally but are locally determined.

    22. What was the actual change in the number of category A responses within 8 minutes between 2010 and 2011?
    • 0
    0

    Explanation

    The correct answer is A.

    In 2011, 2.23×0.749=1.67 category A calls were responded to within 8 minutes. In 2010, 2.08×0.743=1.54. Therefore the change in the number of category A responses within 8 minutes between 2010 and 2011 was 1.67-1.54=0.13, which is closest to the answer option A, 0.12.

    Post Comment

    A student has been carrying out tests to see how well young children can follow instructions.

    A group of children have been colouring in squares on a 4×4 grid. They had been given details of which ones to colour. The student forgot to mark the grids to show the top and bottom and so when the grids were collected for evaluation they needed to be rotated in order to find out which ones were identical to others in the batch. The diagrams below show cards collected from children with 100% success in following their instructions.

    23. How many different patterns were created?
    • 0
    0

    Explanation

    The correct answer is B.

    Numbering the cards shown from left to right, the cards which are identical (can be superimposed) are:

    1 and 3 and 8 and 10

    6 and 7 and 11

    4 and 12

    2 and 9

    5 and no other card

    Hence there are 5 different cards.

    Post Comment

    Police should be given clear permission to use water cannons against rioters and rules about when it is appropriate. Police see water cannons as an effective means of dispersal in some scenarios, incurring fewer injuries to the public than either uncontrolled rioting or other methods of control. In dealing with street riots in major cities last year, police wasted valuable time waiting for overall direction from politicians who fear that inappropriate use of water cannons might antagonise the general public. Clear guidelines could be agreed about using water cannons, for example to deal with rioters who throw missiles and petrol bombs and also where fire and ambulance crews are under threat.

    24. Which of the following, if true, would most strengthen the argument in the passage above?
    • 0
    0

    Explanation

    The correct answer is E.

    The main conclusion of the passage is that police should be allowed to use water cannons against rioters and therefore need to have clear instructions and guidelines as to when they can use them.

    Statement E is the best statement from all of the given options as it supports the use of water cannons.

    Statement A, C & D weaken the argument and are therefore incorrect.

    Statement B is irrelevant as there is link as to when police would be allowed to use water canons.

    Post Comment

    In a variation of the game of darts, players throw their darts at a board which has three non- overlapping circles on it. The circular regions have values of 2 points, 4 points and 6 points, as shown in the diagram below:

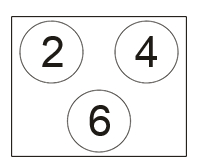
    On each turn a player throws three darts and once all three darts have been thrown their score is added to the player’s overall score. If a dart lands in a circle then the player scores the value of that circle, but if the dart lands outside all of the circles then the player’s score for the turn so far is halved. If two or more darts land outside the circles then the player scores zero. The first player to score 101 points wins the game.

    25. How many different scores in a full turn, apart from 0, are possible?
    • 0
    4

    Explanation

    The correct answer is C.

    Post Comment
    Omar Hussein Medicmind Tutor

    Sun, 16 Oct 2022 12:09:15

    Any possible explanation for this question? I am not sure how to approach it

    Mary Medicmind Tutor

    Fri, 23 Feb 2024 03:11:00

    Kindly explain the answer to this qs

    Is forgery ‘art’? Received opinion says not, despite it unquestionably being a craft. This has nothing to do with it being illegal or immoral, though it may be both. The standard objection is that it is copying, and therefore not creative. But how is that an objection when all art is ultimately a copy of something? Is a picture of a ship or a hay-wagon or a bowl of fruit not art? If all art is copying, then forgery, by definition, is art.

    26. Which one of the following makes the same reasoning error as the above argument?
    • 0
    0

    Explanation

    The correct answer is D.

    The argument is saying that if all art is copying, then forgery (which is considered copying), must therefore be art as well. Just because copying and forgery are both regarded as being art, that copying and forgery are therefore synonymous. This error in the argument structure is presented in statement D.

    Post Comment

    When customers buy any furniture from Ben’s shop they pay half the price of the furniture immediately, one quarter of the price in the next month and the remainder in the month after that.

    The table shows the money that Ben has been paid for the first half of this year.

    January

    		 February March April May June
    $9000 $3000 $4000 $5000 $3000

    $2000

    Ben closed the store for the whole of May and June, so the $5000 in those two months all came from sales in the earlier months.

    27. What is the total value of the furniture that Ben sold between January and June?
    • 0
    4

    Explanation

    The correct answer is C.

    Post Comment
    balls Medicmind Tutor

    Sat, 14 Oct 2023 11:25:33

    How tf

    The ski holiday industry has been accused of damaging the environment. But this is nonsense. If you say that we should stop people skiing, you would have to conclude that we should stop everyone going on holiday. What causes the glaciers to melt is not skiing, it’s everyone wasting energy by travelling when they don’t need to. It has been calculated that tourist transport to and from a ski resort accounts for 74% of the resort’s energy consumption, so the amount of energy used in the resorts themselves is relatively small. Because many ski lifts are run on renewable energy, people may actually be responsible for the production of less CO2 when they are on the ski slopes than in their daily lives back home.

    1. The fact that all travel damages the environment does not prove that the ski holiday industry does not damage the environment.

    2. 26% of a ski resort’s energy consumption may be a high amount of energy compared with other types of resort.

    3.The ski holiday industry may damage the environment in ways unrelated to the level of energy consumption.

    28. Which of the following identifies a weakness in the above argument?
    • 0
    0

    Explanation

    The correct answer is G.

    Statement 1 is correct because the author states that transportation to ski resorts accounts for 74% of a ski resort’s energy consumption. This argument is weakened because even if travel damages the environment, it may still be that the ski industry may continue to destroy the environment (other than through transportation).

    Statement 2 is correct as this weakens the argument that energy consumption levels in other ski resorts are normally lower.

    Statement 3 weakens the conclusion as the author only mentions energy consumption as a form that is destroying the environment. However, there may be other factors to consider.

    Post Comment

    Tickets for a “Sounds of the Seventies” concert held last week cost £20 and had to be purchased in advance. However, on the night, anyone who arrived in 1970s costume was given a £5 refund at the door.

    Exactly 40% of those who bought a ticket wore 1970s clothes, and the income from ticket sales after refunds was £12,240.

    29. What was the total amount refunded to those wearing 1970s clothes?
    • 0
    0

    Explanation

    The correct answer is C.

    If we let y=the total number of tickets sold, we can form the equation:

    20y-0.40(5y)=12240

    20y-2y=12240

    18y=12240

    y=12240/18=680

    Therefore 680 tickets were sold. 

    Hence 680×0.40=272 people wore 1970s clothes and were refunded £5 each.

    So 272×5=£1360 was refunded

    Post Comment

    Authors of articles on health and medical treatments may be sponsored by pharmaceutical companies, by receiving a fee or financial support for their research. The public need to know what weight they should put on these articles when they are assessing evidence from various In the USA, newspapers and broadcasting companies are legally obliged to declare potential conflicts of interest of authors or contributors. We should introduce the same law in the UK.

    1. Authors who receive fees from pharmaceutical companies give a one-sided view of the effectiveness and safety of new medical treatments.

    2. Companies that sponsor authors of articles on medical treatments aim to influence the content of the articles.

    3. The reliability of articles on medical treatments cannot be fairly judged without information about sponsorship by pharmaceutical companies.

    30. Which of the following are assumptions underlying the above argument?
    • 0
    1

    Explanation

    The correct answer is C.

    The passage is arguing that articles cannot be assessed properly until they know how much they are being financed and therefore the assumption is that we cannot judge articles without information on sponsorship from pharmaceutical companies.

    Statement 1 is incorrect because the passage doesn’t mention safety or effectiveness.

    Statement 2 is incorrect because the passage doesn’t mention this either.

    Post Comment

    In each round of a competition the competitor who performed best in that round is awarded 6 points. The next best competitor gets 3 points and the third gets 1 point. There are four competitors, so the last player does not score any points. After 10 rounds the scores are totalled. After nine rounds had been completed, Jill knew that, regardless of the outcome of the final round there would be no ties and she would finish in third place. She also knew that whoever finished ahead out of Karen and Gemma would be the overall winner.

    31. What is the highest score that the last placed player could finish with after all ten rounds are played?
    • 0
    1

    Explanation

    The correct answer is C.

    Post Comment
    John10240525 Medicmind Tutor

    Sun, 24 Oct 2021 10:04:58

    where are the explanations???

    pop Medicmind Tutor

    Sun, 24 Oct 2021 10:05:11

    where is asnwer

    lol Medicmind Tutor

    Fri, 29 Oct 2021 02:03:58

    answer??

    elend123 Medicmind Tutor

    Tue, 11 Jan 2022 10:12:10

    The total score in a round is 10 (6+3+1+0), so over 10 rounds there is 100 points that can be distributed to candidates. 19 is the answer, because the other candidates get 20,20,20,21 and finish before last place. The highest last score cannot be 21, because there is not enough points for 5players to get >=21.

    Are Britain’s roads getting safer? By Lucy Wilkins, BBC News

    The first recorded road death in a motor accident in Britain was in London over 100 years ago. More than a century on, roads may be busier than ever – but are they any safer?

    On 17 August, 1896, a South London housewife entered the history books by being run over. Bridget Driscoll, 44, became the first person recorded to have died in a motor accident in Britain. The 20-year-old driver was a car company worker, and there were reports he had adjusted the engine to increase its maximum speed to 8mph. Ever since that first death – and the first recorded death of a driver 18 months later – the number of vehicles on the roads has multiplied.

    Increasing number of vehicles

    According to the Department for Transport (DfT), in 1930 there were only 2.3 million motor vehicles in Great Britain, but more than 7,000 people were killed in road accidents. In contrast nowadays there are more vehicles but fewer deaths – there are 27 million vehicles and 3,180 people were killed in the 12 months to March this year, provisional results show.

    The DfT is meeting its 10-year safety target of cutting the number of road accident deaths and injuries to 40% of the 1994-98 average – 319,928 casualties. Five years into the policy, the statistics show casualties are 33% below the earlier average. In actual numbers, 268,900 people were either injured or killed in the 12 months to this March.

    But are Britain’s roads really becoming safer? The statistics paint a confusing picture Many road accidents, where there are slight injuries or even more severe ones, bypass police records. This could be because some of the people involved in accidents do not want to tell the police because they are uninsured, unlicensed, or drunk, says head of road safety at the AA Motoring Trust, Andrew Howard. But even if injuries are reported, it does not mean the police will record them. The severity of the injury will also be under-estimated, research in the 1990s suggested.

    “The combined effect of under-reporting, under-recording and misclassification suggests that there may be 2.76 times as many killed or seriously injured casualties than are recorded in the national casualty figures and 1.70 times as many slight casualties,” the DfT says.

    In June, three Oxford University researchers queried the figures after comparing them to hospital admissions from road accidents. The DfT statistics, from the police and including all hospital admissions, showed a fall from 85.9 people killed or seriously injured per 100,000 in 1996 to 59.4 per 100,000 in 2004. However, hospital admissions were almost unchanged at 90 per 100,000 in 1996 and 91.1 in 2004. They said the disparity was probably due to under- reporting and/or fewer minor injuries.

    Statistical ‘utopia’

    Paul Smith, from Safe Speed, said: “For every 100 accidents reported, there’s 180 that aren’t reported.” Cars are safer, paramedics better trained, there are more air ambulances and roads have improved, said Mr Smith. The only factor that has not changed is drivers who “are getting worse” in his opinion. He urged the department to focus on educating drivers about their responsibilities, rather than just getting them to drive slower.

    But Mr Howard, from the AA Motoring Trust, is encouraged by the statistics: “My view, and I would say this is true of most of those involved in road safety, is that the statistics do show the roads are getting safer.”

    32. By what factor is the reported annual number of deaths per vehicle on the road higher or lower at the time of the above report than it was in 1930?
    • 0
    0

    Explanation

    The correct answer is A.

    In 1930 there were 7000/2300000=0.00304 deaths per vehicle and at the time of the report there were 3180/27000000=0.000117 deaths per vehicle. So at the time of the report compared to in 1930, the number of deaths per vehicle was 0.000117/0.00304=0.04 times as much.

    Post Comment

    Are Britain’s roads getting safer? By Lucy Wilkins, BBC News

    The first recorded road death in a motor accident in Britain was in London over 100 years ago. More than a century on, roads may be busier than ever – but are they any safer?

    On 17 August, 1896, a South London housewife entered the history books by being run over. Bridget Driscoll, 44, became the first person recorded to have died in a motor accident in Britain. The 20-year-old driver was a car company worker, and there were reports he had adjusted the engine to increase its maximum speed to 8mph. Ever since that first death – and the first recorded death of a driver 18 months later – the number of vehicles on the roads has multiplied.

    Increasing number of vehicles

    According to the Department for Transport (DfT), in 1930 there were only 2.3 million motor vehicles in Great Britain, but more than 7,000 people were killed in road accidents. In contrast nowadays there are more vehicles but fewer deaths – there are 27 million vehicles and 3,180 people were killed in the 12 months to March this year, provisional results show.

    The DfT is meeting its 10-year safety target of cutting the number of road accident deaths and injuries to 40% of the 1994-98 average – 319,928 casualties. Five years into the policy, the statistics show casualties are 33% below the earlier average. In actual numbers, 268,900 people were either injured or killed in the 12 months to this March.

    But are Britain’s roads really becoming safer? The statistics paint a confusing picture Many road accidents, where there are slight injuries or even more severe ones, bypass police records. This could be because some of the people involved in accidents do not want to tell the police because they are uninsured, unlicensed, or drunk, says head of road safety at the AA Motoring Trust, Andrew Howard. But even if injuries are reported, it does not mean the police will record them. The severity of the injury will also be under-estimated, research in the 1990s suggested.

    “The combined effect of under-reporting, under-recording and misclassification suggests that there may be 2.76 times as many killed or seriously injured casualties than are recorded in the national casualty figures and 1.70 times as many slight casualties,” the DfT says.

    In June, three Oxford University researchers queried the figures after comparing them to hospital admissions from road accidents. The DfT statistics, from the police and including all hospital admissions, showed a fall from 85.9 people killed or seriously injured per 100,000 in 1996 to 59.4 per 100,000 in 2004. However, hospital admissions were almost unchanged at 90 per 100,000 in 1996 and 91.1 in 2004. They said the disparity was probably due to under- reporting and/or fewer minor injuries.

    Statistical ‘utopia’

    Paul Smith, from Safe Speed, said: “For every 100 accidents reported, there’s 180 that aren’t reported.” Cars are safer, paramedics better trained, there are more air ambulances and roads have improved, said Mr Smith. The only factor that has not changed is drivers who “are getting worse” in his opinion. He urged the department to focus on educating drivers about their responsibilities, rather than just getting them to drive slower.

    But Mr Howard, from the AA Motoring Trust, is encouraged by the statistics: “My view, and I would say this is true of most of those involved in road safety, is that the statistics do show the roads are getting safer.”

    33. There is disagreement in the article about whether roads are becoming more or less safe. In addition to the reasons given in the text, which one of the following, if true, would strengthen the case for roads becoming safer?
    • 0
    0

    Explanation

    The correct answer is D.

    A would suggest that there are additional road accidents that have not been reported in the data shown, implying that roads have become less safe, so A actually weakens the case for roads becoming safer.

    B suggests that less injuries are sustained now than in the past, but not that there are fewer accidents, so does not indicate that roads have become safer, only that we have more protection by cars.

    C actually weakens the argument by suggesting that there are fewer reported incidents per road accident, so roads may be just as dangerous or even more than in the past.

    E suggests that there are now fewer deaths per road accident because people are less likely to die from trauma in a road accident, but again does not indicate that there are fewer accidents or how road safety has changed.

    Therefore the answer is D, because if recording of road accidents have become more accurate, the data that supports the idea that road safety has improved is more likely to be reliable.

    Post Comment

    Are Britain’s roads getting safer? By Lucy Wilkins, BBC News

    The first recorded road death in a motor accident in Britain was in London over 100 years ago. More than a century on, roads may be busier than ever – but are they any safer?

    On 17 August, 1896, a South London housewife entered the history books by being run over. Bridget Driscoll, 44, became the first person recorded to have died in a motor accident in Britain. The 20-year-old driver was a car company worker, and there were reports he had adjusted the engine to increase its maximum speed to 8mph. Ever since that first death – and the first recorded death of a driver 18 months later – the number of vehicles on the roads has multiplied.

    Increasing number of vehicles

    According to the Department for Transport (DfT), in 1930 there were only 2.3 million motor vehicles in Great Britain, but more than 7,000 people were killed in road accidents. In contrast nowadays there are more vehicles but fewer deaths – there are 27 million vehicles and 3,180 people were killed in the 12 months to March this year, provisional results show.

    The DfT is meeting its 10-year safety target of cutting the number of road accident deaths and injuries to 40% of the 1994-98 average – 319,928 casualties. Five years into the policy, the statistics show casualties are 33% below the earlier average. In actual numbers, 268,900 people were either injured or killed in the 12 months to this March.

    But are Britain’s roads really becoming safer? The statistics paint a confusing picture Many road accidents, where there are slight injuries or even more severe ones, bypass police records. This could be because some of the people involved in accidents do not want to tell the police because they are uninsured, unlicensed, or drunk, says head of road safety at the AA Motoring Trust, Andrew Howard. But even if injuries are reported, it does not mean the police will record them. The severity of the injury will also be under-estimated, research in the 1990s suggested.

    “The combined effect of under-reporting, under-recording and misclassification suggests that there may be 2.76 times as many killed or seriously injured casualties than are recorded in the national casualty figures and 1.70 times as many slight casualties,” the DfT says.

    In June, three Oxford University researchers queried the figures after comparing them to hospital admissions from road accidents. The DfT statistics, from the police and including all hospital admissions, showed a fall from 85.9 people killed or seriously injured per 100,000 in 1996 to 59.4 per 100,000 in 2004. However, hospital admissions were almost unchanged at 90 per 100,000 in 1996 and 91.1 in 2004. They said the disparity was probably due to under- reporting and/or fewer minor injuries.

    Statistical ‘utopia’

    Paul Smith, from Safe Speed, said: “For every 100 accidents reported, there’s 180 that aren’t reported.” Cars are safer, paramedics better trained, there are more air ambulances and roads have improved, said Mr Smith. The only factor that has not changed is drivers who “are getting worse” in his opinion. He urged the department to focus on educating drivers about their responsibilities, rather than just getting them to drive slower.

    But Mr Howard, from the AA Motoring Trust, is encouraged by the statistics: “My view, and I would say this is true of most of those involved in road safety, is that the statistics do show the roads are getting safer.”

    34. The second section refers to a DfT 10 year target. To the nearest 1000, what is the DfT’s target?
    • 0
    0

    Explanation

    The correct answer is C.

    The target is 40% of 319928 casualties: 32000×0.40=128000.

    Post Comment

    Are Britain’s roads getting safer? By Lucy Wilkins, BBC News

    The first recorded road death in a motor accident in Britain was in London over 100 years ago. More than a century on, roads may be busier than ever – but are they any safer?

    On 17 August, 1896, a South London housewife entered the history books by being run over. Bridget Driscoll, 44, became the first person recorded to have died in a motor accident in Britain. The 20-year-old driver was a car company worker, and there were reports he had adjusted the engine to increase its maximum speed to 8mph. Ever since that first death – and the first recorded death of a driver 18 months later – the number of vehicles on the roads has multiplied.

    Increasing number of vehicles

    According to the Department for Transport (DfT), in 1930 there were only 2.3 million motor vehicles in Great Britain, but more than 7,000 people were killed in road accidents. In contrast nowadays there are more vehicles but fewer deaths – there are 27 million vehicles and 3,180 people were killed in the 12 months to March this year, provisional results show.

    The DfT is meeting its 10-year safety target of cutting the number of road accident deaths and injuries to 40% of the 1994-98 average – 319,928 casualties. Five years into the policy, the statistics show casualties are 33% below the earlier average. In actual numbers, 268,900 people were either injured or killed in the 12 months to this March.

    But are Britain’s roads really becoming safer? The statistics paint a confusing picture Many road accidents, where there are slight injuries or even more severe ones, bypass police records. This could be because some of the people involved in accidents do not want to tell the police because they are uninsured, unlicensed, or drunk, says head of road safety at the AA Motoring Trust, Andrew Howard. But even if injuries are reported, it does not mean the police will record them. The severity of the injury will also be under-estimated, research in the 1990s suggested.

    “The combined effect of under-reporting, under-recording and misclassification suggests that there may be 2.76 times as many killed or seriously injured casualties than are recorded in the national casualty figures and 1.70 times as many slight casualties,” the DfT says.

    In June, three Oxford University researchers queried the figures after comparing them to hospital admissions from road accidents. The DfT statistics, from the police and including all hospital admissions, showed a fall from 85.9 people killed or seriously injured per 100,000 in 1996 to 59.4 per 100,000 in 2004. However, hospital admissions were almost unchanged at 90 per 100,000 in 1996 and 91.1 in 2004. They said the disparity was probably due to under- reporting and/or fewer minor injuries.

    Statistical ‘utopia’

    Paul Smith, from Safe Speed, said: “For every 100 accidents reported, there’s 180 that aren’t reported.” Cars are safer, paramedics better trained, there are more air ambulances and roads have improved, said Mr Smith. The only factor that has not changed is drivers who “are getting worse” in his opinion. He urged the department to focus on educating drivers about their responsibilities, rather than just getting them to drive slower.

    But Mr Howard, from the AA Motoring Trust, is encouraged by the statistics: “My view, and I would say this is true of most of those involved in road safety, is that the statistics do show the roads are getting safer.”

    35. Which one of the following could explain the discrepancy between the DfT statistics and hospital admissions for deaths and serious injuries on the road?
    • 0
    0

    Explanation

    The correct answer is A.

    Hospital admissions for death and serious injuries on the road is greater than that for the DfT statistics. This could be because either the hospital statistics are overestimating or the DfT statistics are underestimating. The second option is given by A.

    Post Comment

    BMAT 2012 S1 Review Screen

    Instructions

    Below is a summary of your answers. You can review your questions in three (3) different ways.

    The buttons in the lower right-hand corner correspond to these choices:

    1. Review all of your questions and answers.
    2. Review questions that are incomplete.
    3. Review questions that are flagged for review. (Click the 'flag' icon to change the flag for review status.)

    You may also click on a question number to link directly to its location in the exam.

    BMAT 2012 S1 Section

    Final Answer Review Screen

    Instructions

    This review section allows you to view the answers you made and see whether they were correct or not. Each question accessed from this screen has an 'Explain Answer' button in the top left hand side. By clicking on this you will obtain an explanation as to the correct answer.

    At the bottom of this screen you can choose to 'Review All' answers, 'Review Incorrect' answers or 'Review Flagged' answers. Alternatively you can go to specific questions by opening up any of the sub-tests below.

    BMAT 2012 S1 Section

    x

    +/-
    √
    %
    MRC
    M-
    M+
    7
    8
    9
    4
    5
    6
    1
    2
    3
    ON/C
    0
    .
    ÷
    ×
    -
    +
    =

    Let's get acquainted ?
    What is your name?

    Next

    Nice to meet you, {{name}}!
    What is your preferred phone number?

    What is your preferred phone number?

    Next

    Just to check, what are you interested in?

    1-1 Tutoring Online Course Bursaries/Resources Other

    When should we call you?

    Another Day
    Skip the Call

    What time works best for you? (UK Time)

    8am-2pm 2pm-10pm
    10:00-10:30 10:30-11:00 11:00-11:30 11:30-12:00 12:00-12:30 12:30-13:00
    15:00-15:30 15:30-16:00 16:00-16:30 16:30-17:00 17:00-17:30 17:30-18:00 18:00-18:30 18:30-19:00 19:00-19:30 19:30-20:00

    How many hours of 1-1 tutoring are you looking for?

    0-5 10 20-30 40+

    My WhatsApp number is...

    Same as the one I entered Different to the one I entered

    For our safeguarding policy, please confirm...

    For our safeguarding policy, please confirm...

    I am under 18 I am over 18

    Which online course are you interested in?

    Next

    What is your query?

    Submit

    You can apply for a bursary by clicking this link

    https://www.medicmind.co.uk/medic-mind-foundation/

    Sure, what is your query?

    Submit

    Loading...

    Thank you for your response.
    We will aim to get back to you within 12-24 hours.

    Lock in a 2 Hour 1-1 Tutoring Lesson Now

    If you're ready and keen to get started click the button below to book your first 2 hour 1-1 tutoring lesson with us. Connect with a tutor from a university of your choice in minutes. (Use FAST5 to get 5% Off!)

    Buy Now for £70